Abstract
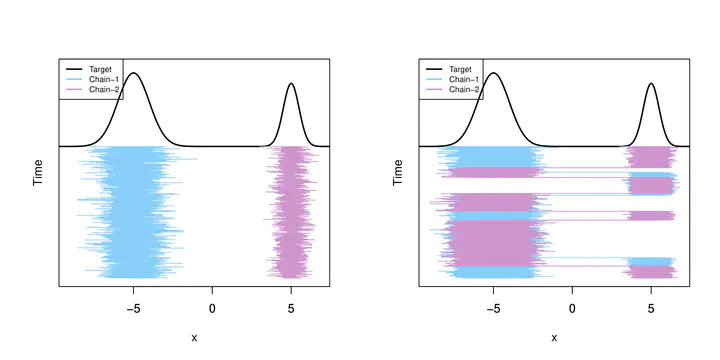
Autocovariances are a fundamental quantity of interest in Markov chain Monte Carlo (MCMC) simulations with autocorrelation function (ACF) plots being an integral visualization tool for performance assessment. Unfortunately, for slow-mixing Markov chains, the empirical autocovariance can highly underestimate the truth. For multiple-chain MCMC sampling, we propose a globally-centered estimator of the autocovariance function (G-ACvF) that exhibits significant theoretical and empirical improvements. We show that the bias of the G-ACvF estimator is smaller than the bias of the current state-of-the-art. The impact of this improved estimator is evident in three critical output analysis applications - (1) ACF plots, (2) estimates of the Monte Carlo asymptotic covariance matrix, and (3) estimates of the effective sample size. Under weak conditions, we establish strong consistency of our improved asymptotic covariance estimator, and obtain its large-sample bias and variance. The performance of the new estimators is demonstrated through various examples.